阅读:0
听报道
新型冠状病毒疫情,牵动着全国人们的心。疫情暴发以来,很多机构都给出了疫情走向的预测结果,有些结果相对客观,有些结果则甚至惊动了国家卫健委的专家。
对于我们普通人来说,因为疫情的走势时刻在变化,而且有政府防疫工作的强力介入,因此过去的模型结果,随着时间的推移,往往会变得不可靠,因此了解预测模型背后的逻辑和参数,更重要。但是我们又无法要求专家们时刻更新他们的模型,因此就需要我们自己尝试搭建一些简单的模型,以便于更及时的跟踪疫情走势。
笔者在网上搜集了一些模型资料,不过大部分模型是用MATLAB写的,对于普通人来说,购买MATLAB的价格太贵。因此在本文中,笔者尝试用免费的R,写出几个经典的传染病模型的仿真代码,后续我们可以不断添加各种条件,来继续完善。
下文中的动力学模型,基本上都会用到微分方程,有些方程有解析解,有些方程没有解析解。我们不会算解析解也没有关系。我们只需要把微分方程形式、初始值和参数输入R,R就会帮我们做出数值解。
模型一:自由增长模型
模型假设

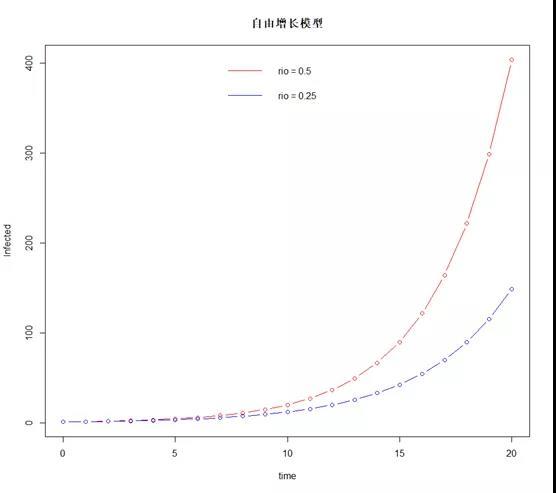
我们设置每个病人、每天传染的人数的常数rio,分别为0.3和0.25,设置初期只有1个病人,来看看模拟的传染人数。从下图可以看到,自由增长模型整体上呈现指数增长趋势,对参数rio非常敏感。这种模型比较适合,古代医疗条件不发达、不懂得对病人进行防疫隔离时,发生恶性瘟疫的情形。


模型二:SI模型
模型假设
在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移;
人群分为易感染者(Susceptible)和已感染者(Infective)两类(取两个词的首字母,称之为SI模型);
每个病人每天有效接触的平均人数是常数,称为日接触率;
当病人与健康者有效接触时,使健康者受感染变为病人。

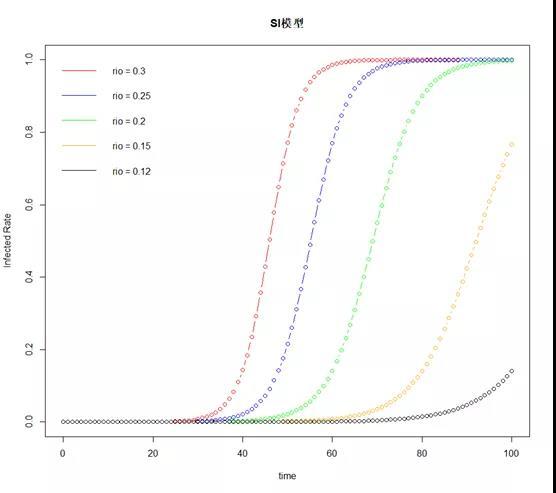
我们设置每个病人、每天接触的人数的常数rio,分别为0.3、0.25、0.2、0.15、0.12,设置初期感染率为百万分之一,0.000001,来看看模拟的感染者比例。
从下图可以看到,SI模型对参数rio非常敏感,而且只要我们把每个病人、每天接触的人数有效降低,传染病的传染速度就会变得非常慢,这就意味着,只要防疫力度够大,控制住传染病是完全可能的。这种模型比较适合,被传染后无法恢复健康的,比如HIV等情形。



模型三:SIS模型
SIS模型与SI模型的差异,在于SIS模型假设已感染者(Infective)可以被治愈,重新变成易感染者(Susceptible),比如季节性流感等。
模型假设
在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移;
人群分为易感染者(Susceptible)和已感染者(Infective)两类,已感染者(Infective)可以被治愈,变成易感染者(Susceptible)(称之为SIS模型);
每个病人每天有效接触的平均人数是常数,称为日接触率;
当病人与健康者有效接触时,使健康者受感染变为病人;
每天被治愈的病人数,占病人总数的比例为常数μ,称为日治愈率;
那么,病人被全部治愈,所需要的天数为1/μ,这就是传染病的平均传染期。

SIS模型中有两个参数,分别是每个病人每天有效接触的平均人数rio,以及每天被治愈的病人比例mu,我们设置mu为0.1,每个病人、每天接触的人数的常数rio,分别为0.27、0.25、0.20、0.15、0.12,设置初期感染率为百万分之一,0.000001,来看看模拟的感染者比例。
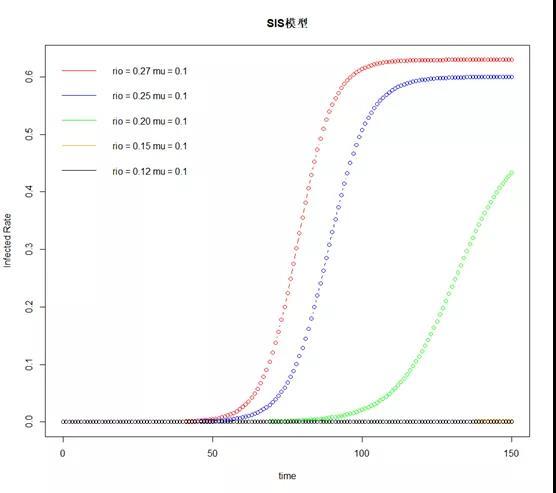
从上图可以看到,对于SIS模型而言:
1、传染的速度,取决于病人的传染速度,与病人的治愈速度之间的相对水平,如果病人的治愈速度,大于病人的传染速度,那么该传染病最终会消失;
2、即便病人的传染速度高于治愈速度,最终也只有一部分人群会被感染;
3、最终感染的人群比例,为1-1/sigma,sigma = rio/mu,sigma是整个传染期内每个病人的有效接触人数,可以理解为病人在整个生病期内,接触的总人数。


模型四:SIR模型
SIR模型与SIS模型的差异,在于SIR模型假设已感染者(Infective)被治愈后会具备免疫力,不会被感染,从而成为移出者(Removed),SIR模型已经初步接近实际的传染病模型。
模型假设
在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移;
人群分为易感染者(Susceptible)、已感染者(Infective)和移出者(Removed)三类;
每个病人每天有效接触的平均人数是常数,称为日接触率;
当病人与健康者有效接触时,使健康者受感染变为病人;
每天被治愈的病人数,占病人总数的比例为常数μ,称为日治愈率;
那么,病人被全部治愈,所需要的天数为1/μ,这就是传染病的平均传染期。

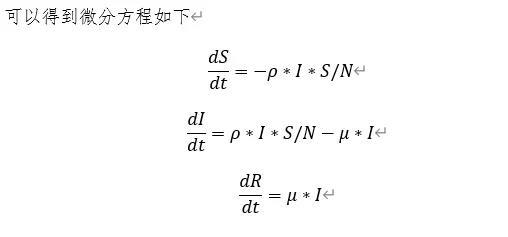
疫情刚开始的时候,于晓华教授曾经用SIR做了一个模拟,我们现在用于晓华教授的参数,把于教授的结果复制出来如下。从下图来看,还是比较契合的。
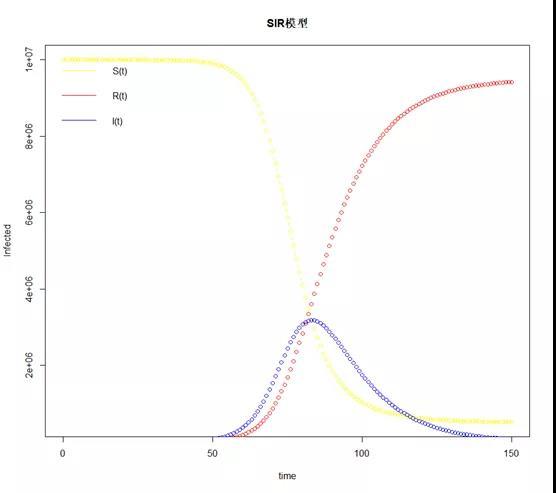
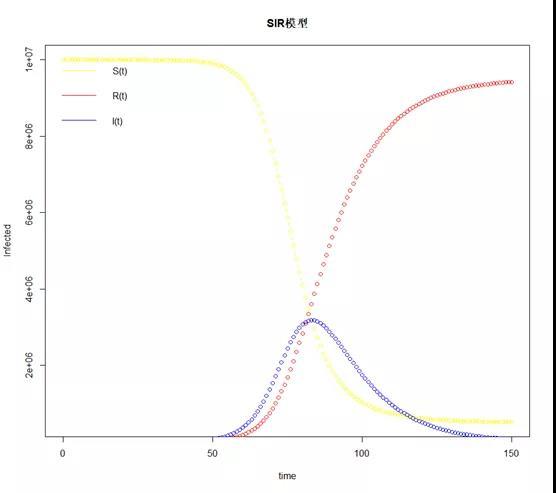


对本轮疫情走势的密切跟踪,是研判本轮疫情冲击,必不可少的工作。我们在本文中讨论了几个经典的传染病模型,并用R做了模拟。其中SIR模型已经开始接近现实模型,我们也复制出了于晓华教授的结果。
后续我们会进一步考虑潜伏期等问题,进一步完善模型,并尝试根据疫情的进展,不断调试我们的模型参数,来密切跟踪疫情进展。如果有感兴趣的读者朋友,也随时欢迎留言或者后台私信,进行合作讨论。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 