阅读:0
听报道
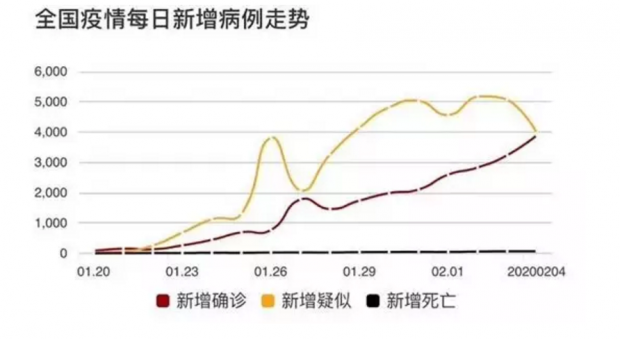
今天早上,笔者看到很多朋友在转发一个图。图中显示,每日新增疑似病例数,出现了较大幅度的回落,预示着疫情走势出现好转。
我们在前文《几个经典的传染病模型及其R实现》,介绍了传染病动力学的经典模型。在前文《一个研判疫情走向的简单方法》,给了一个研判疫情的简单方法。在前文《如何看待央行下调公开市场操作利率10BP?(基于北京流行病学分析的一个视角)》,做了北京病例的流行病学分析。
我们再提出一个问题,如果拿到了今天的疫情数据,比如今天的疑似病例数,能否更好的预测明天乃至未来的确诊病例数呢?我们先来观察一下,新增确诊病例与新增疑似病例之间的关系。
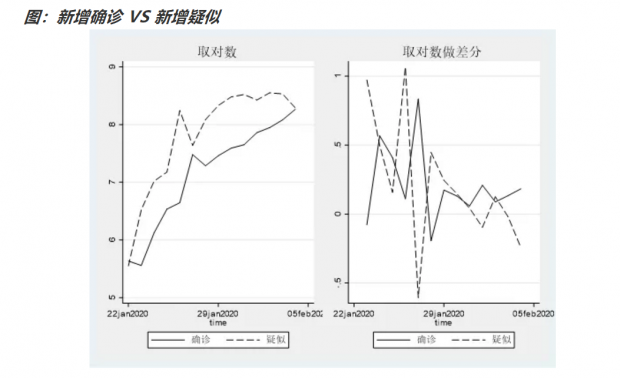
从下图可以看到,新增疑似病例,确实对新增确诊病例,有很好的领先性,从图上观察,领先期大概是一天。那么这个逻辑是好理解的,前一天的疑似病例,在经过肺部CT、核酸检测等步骤后,获得确诊。
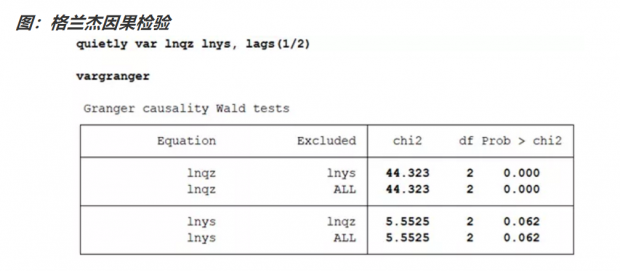
我们来对两者做一个格兰杰因果检验。从格兰杰因果检验上,可以看到,统计意义上,过去的新增疑似病例数,对未来的新增确诊病例数有很显著的影响。
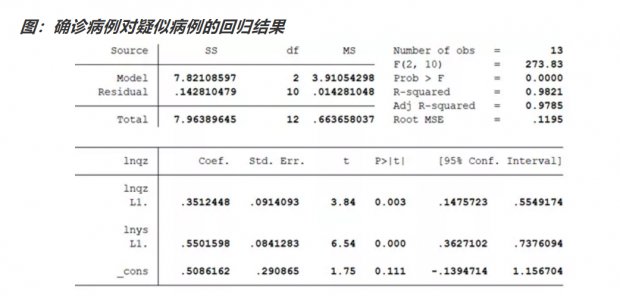
那么我们用滞后一期的新增确诊数和新增疑似数,对当期的新增确诊数做回归。从下表可以看到,滞后一期的新增疑似,对当期的新增确诊有很强的预测意义。
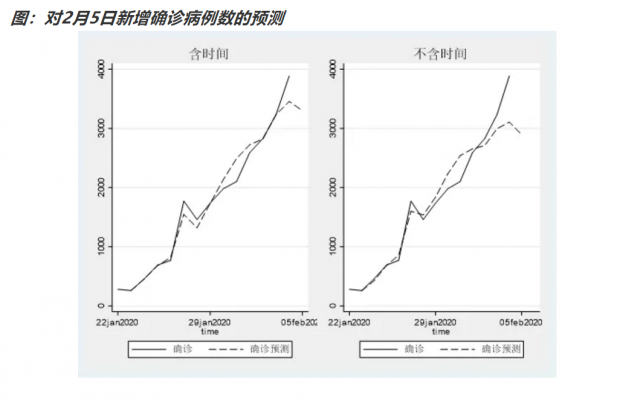
当然,我们也可以把时间变量也同步加入。我们用含时间变量和不含时间变量的回归模型,对明天的新增确诊病例做预测,结果如下图。从下图可以看到,由于今天的新增疑似出现了较大幅度的回落,因此这会带动明天的新增确诊的回落。具体而言,含时间的回归模型,预测2月5月新增确诊病例3299例。不含时间的回归模型,预测2月5月新增确诊病例2895例。
以上就是用滞后变量做回归,来预测未来确诊病例的方法。但是这种方法,只能对未来一期做预测,如果想对未来多期做预测,那就要用的VAR(向量自回归)模型。
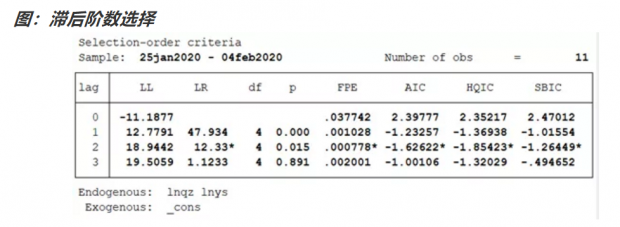
我们先来选择一下滞后的阶数。从下图的结果中可以看到,选择滞后两阶比较合适。
我们以滞后两阶的VAR模型,对未来十期做预测。我们分别做出含时间变量和不含时间变量的预测如下图。
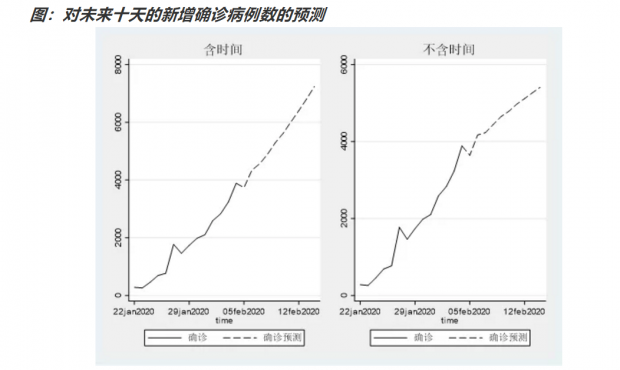
从上图中可以看到,新增确诊病例都是上行的。含时间的模型,上行速度更快些。具体落到2月5日的预测,VAR(2)含时间的预测是3738例,不含时间的预测是3641例。
最后总结一下本文的结论。我们用新增疑似病例数对新增确诊病例数做了含滞后项的回归分析以及VAR模型。从分析结果来看,对未来一期的预测效果不错。基于目前数据,2月5日的新增病例数,会有一个明显的回落。滞后项回归做出的两个结果分别是3299例和2895例。(2月4日是3887例)
但是如果把预测的时间线拉长,我们会发现,预测的新增病例数呈现线性增长,没有出现拐点迹象。因为模型中,不包含限制人员流动、加大床位和医疗力量等,能构成拐点的外生变量。
因此总的来说,盯着新增疑似,可以比较好地预判第二天新增确诊,但无法从新增疑似下降得出拐点将至的结论。对拐点的预测,我们需要构建包含限制人员流动、加大医疗供应等外生变量的VAR模型。我们可以考虑把衡量病毒传染性的R0作为外生变量加入,这是我们下一篇文章要研究的内容。
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 